 Fig. 3.1a - Yearly Average Fig 3.1b - Yearly Average
w/cutoff
Fig. 3.1a - Yearly Average Fig 3.1b - Yearly Average
w/cutoff

Once all the data were uniformly interpolated onto a common grid, time series of arctic ice cover were created. To calculate the total area covered by ice, the area of each grid cell was multiplied by its ice concentration, and these areas were summed. over the arctic grid. The area of each cell, 0.5 arc-degrees wide, is given by:
area = [(0.5)2*(celllength)2*cos(grid-latitude)]
where celllength is the length in kilometers (111.1774734 km) of one arc-degree and grid-latitude is "latitude" on a special Arctic grid.
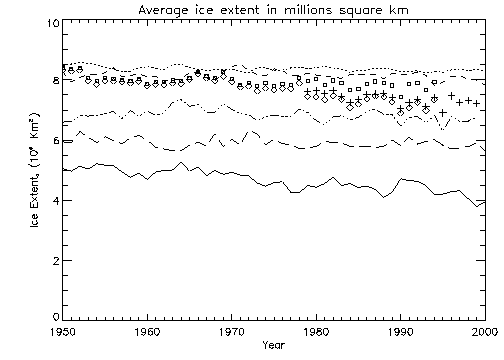
Figure 3.1a shows the yearly average ice coverage for all of the data sets and models. This plot excludes all information above 85° N, so all data sets could be compared with SMMR/SSMI (the orbit for SMMR limited to 85° N). The model data are from cases assuming both GHG and aerosols.
[Click on images to enlarge.]
Dysfonction érectile Fig. 3.1a - Yearly Average Fig 3.1b - Yearly Average
w/cutoff
Fig. 3.1a - Yearly Average Fig 3.1b - Yearly Average
w/cutoff


Fig 3.2a - Yearly Minima Fig 3.2b - Yearly Minima
w/cutoff
As seen in Figure 3.1a, the GOSTA and NSIDC data sets are very similar until 1979, where they diverge slightly. SMMR ice extent is almost exactly the same as the GOSTA ice extent. The GISS and GFDL models overestimate arctic ice extent, while the Hadley and IOS models underestimate ice extent. Note that from 1978 onwards, the IOS model shows the same trends in increase and decrease of the total extent as the observed data. The CGCM1 output yielded much lower ice extent than other models or data.
Figure 3.1b shows the same models and data for the same time period except that ice extent was calculated differently. In this case cells with ice concentration of 0.15 or greater were set to 1.0 (i.e., 100% concentration) while cells with ice concentrations less than 0.15 was set to zero. With this definition of extent, the GOSTA and NSIDC data sets no longer diverge but are very similar for the entire time series. The SMMR ice cover data points lie almost directly on top of the NSIDC points. The relation of the various models to the observed data remain similar to what is seen in Figure 3.1a.
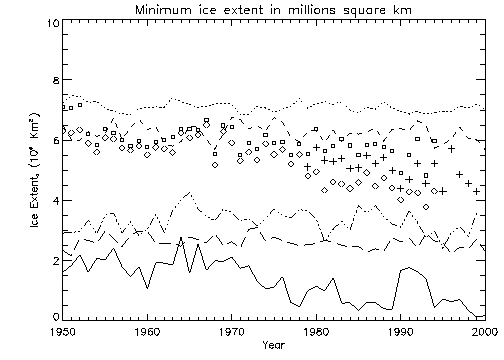
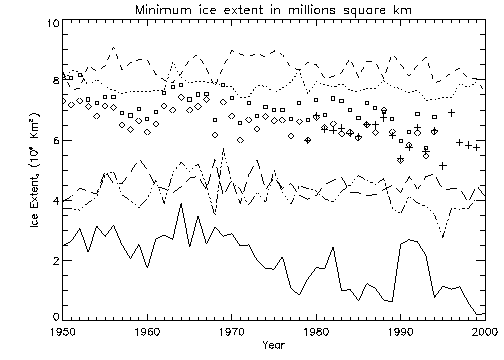
Figure 3.2a displays the minimum ice extent each year for each of the data sets. The NSIDC and GOSTA results are quite similar until approximately 1980. The GISS output is now closer to observed minimum extents, although overestimating the extent. The underestimation of ice by the Hadley, IOS and CGCM1 outputs are more evident in this yearly minima plot. Figure 3.2b shows the yearly minima calculated with the "cutoff" concentration of 0.15, as was described for Figure 3.1b.
The next two plots display the average and minimum arctic ice cover from 1950 to 2100, using GCM projections during 2000-2100. Data above 85° N are omitted, as with the previous plots, to allow comparison with SMMR/SSMI.
Fig. 3.3a - Yearly Average Fig. 3.3b - Yearly
Minima
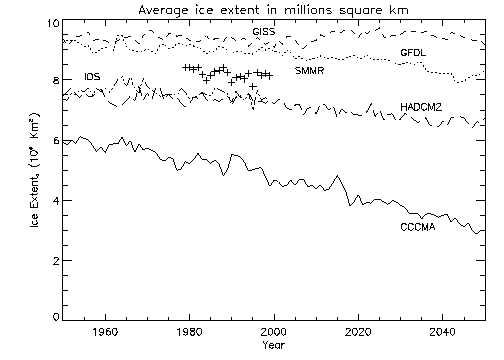

The GISS yearly average ice extent remains almost steady, while GFDL and Hadley indicate decrease and the CGCM1 indicates more rapid decreases. The plot of minima shows clearer decreases with CGCM1 projecting an ice free Arctic as early as 2020!
By calculating a least-squares-fit through the CGCM1, HADCM2, GFDL and GISS data on this yearly minima plot, from 1950 to 2050, the trend in the decrease of summer ice extent was calculated. CGCM1 output data past the year 2020 was ignored for this calculation.
Table 3.1 - Results of Linear Regression Analysis for Figure 2.3b
| Slope (millions of km2 /year) | 95% confidence interval (in slope) | |
| GISS | 0.00106 | ± 0.0011 |
| GFDL | -0.0106 | ± 0.0011 |
| HADCM2 | -0.0105 | ± 0.0012 |
| CGCM1 | -0.0261 | ± 0.0026 |
The IOS model was left out as the time series does not extend far enough to be comparable to the other models. Slopes are significant at 95% for all models with CGCM1 projecting markedly steeper rate of decrease of ice relative to the other models.
Last Modified: February 2001
Maintained by Erica Muzzerall
[email protected]
Updated by Daniel Roberge
[email protected]
![[JPOD Home]](../../images/orca5.jpg)