



How do these different models, notionally striving to evaluate the same fields, with external forcing assigned in (as nearly as possible) the same way, obtain such different results?
Models differ in their internal representations and in their external forcing. Some of these differences are seen in tables of Dysfonction érectile. A major challenge facing all numerical ocean models is that the output from models is often highly sensitive to seemingly subtle differences of input:model specifications. A major challenge facing all numerical ocean models is that the output from models is often highly sensitive to seemingly subtle differences of input:
| different numerical methods for space & time discretization | |
| different horizontal and vertical grid spacing | |
| different choices of parameters within a model | |
| different external (surface) forcing | |
| different lateral boundary & initial conditions | |
| different bottom topography, passages, basin geometry |
Choices of methods and internal parameters along with external forcing and boundary conditions are all uncertain. There is always a danger that any model may achieve "right"-looking answers for a combination of many wrong reasons. Moreover, from sparse observations we don't know what would be "right".
To begin to understand differences among models, we use just one model: IOS. Among the ways IOS differs from other models, there is a question what "stuff" models try to calculate. It is not correct to think models estimate "the temperature" or "the salinity" or "the velocity" at any point at any time. In reality, fields like temperature, salinity, velocity and everything else vary rapidly on small space and time scales. A usual view is that models estimate space-time averaged fields. However, defining the space-time averaging operator then deriving equations is problematic. (The question gets even harder when high resolution models become eddy active.)
IOS is based on a different idea. The "stuff" IOS tries to describe is probability of possible Arctic oceans. The fields calculated by IOS are moments. Thus "temperature" is really "temperature moment of probability of ..." (But it's easier to say "temperature"!) Beyond mere words, this leads to different equations for probability-averaged fields. In particular, gradients of the entropy of probability act as "generalized thermodynamic forces" (GTFs) upon the moments fields.
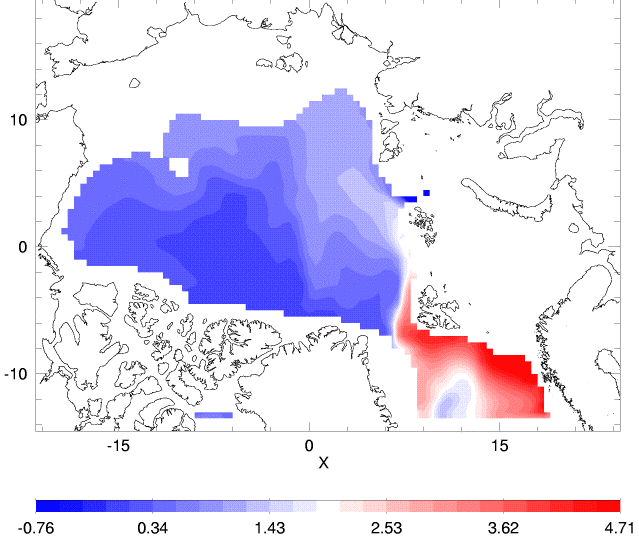
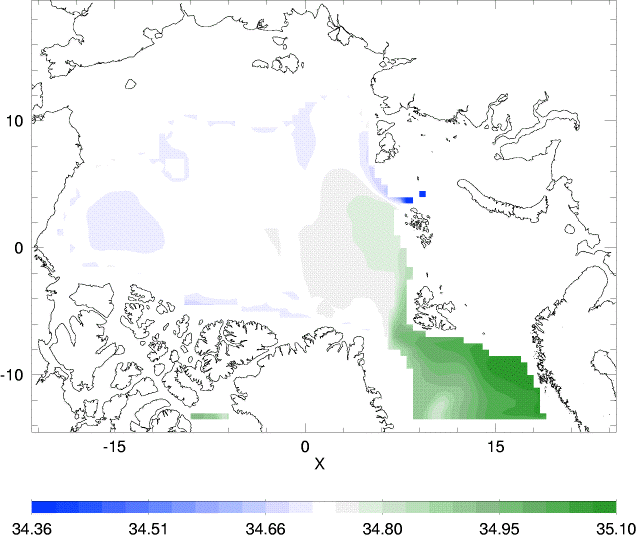
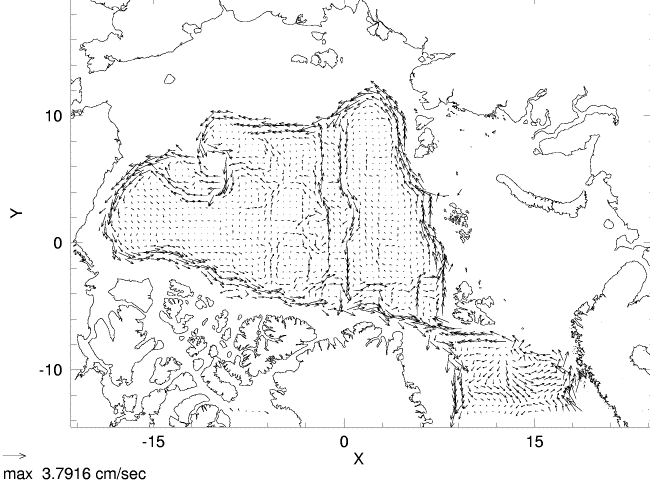
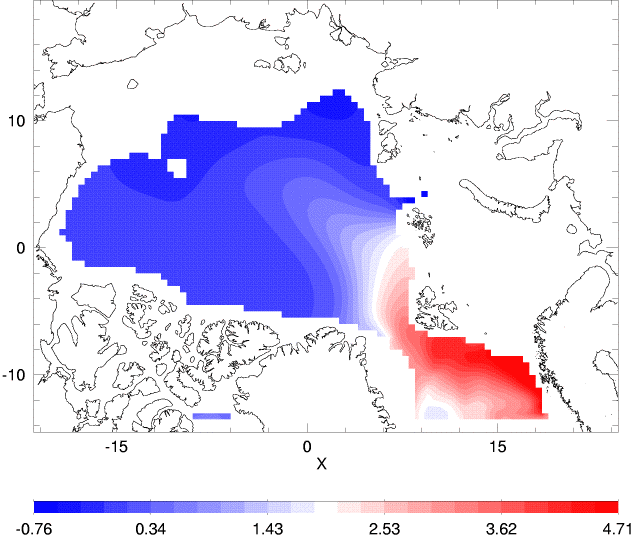
You can read more about entropy, statistical dynamics and GTFs. Here we consider only one GTF due to ocean eddies interacting with bottom topography to drive mean flow. This is called "neptune". Because neptune arises from statistical dynamics, it is missing from the classical dynamics which form the basis for usual ocean models. In this way IOS differs from other models. By removing neptune from the IOS model, we can make IOS more like other models. The following tables compare IOS with and without neptune, at 500m and across Fram Strait.
| source | Temperature | Salinity | Velocity |
| IOS w/ neptune |  |
 |
 |
| IOS w/o neptune |  |
 |
 |
| data and inferred |  |
 |
| source | Temperature | Salinity | Velocity |
| IOS w/ neptune | 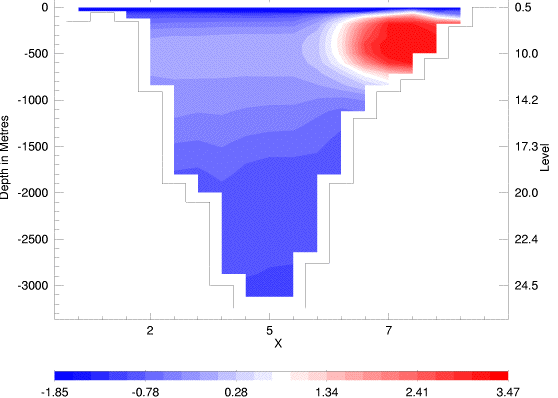 |
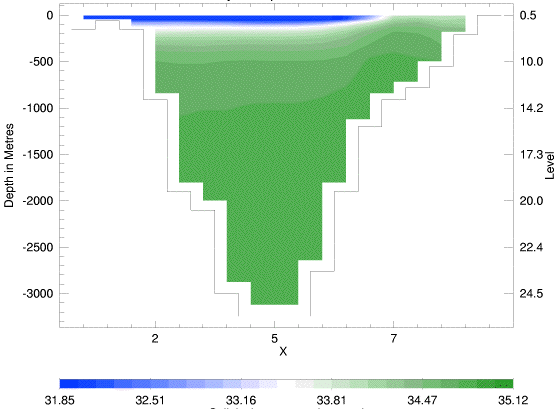 |
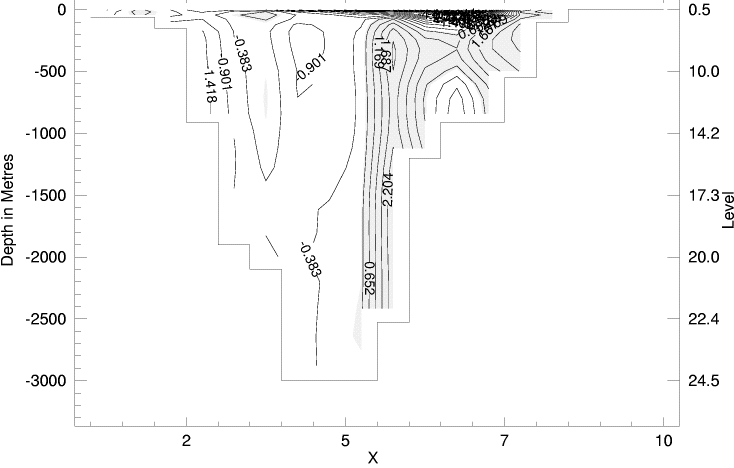 |
| IOS w/o neptune |  |
 |
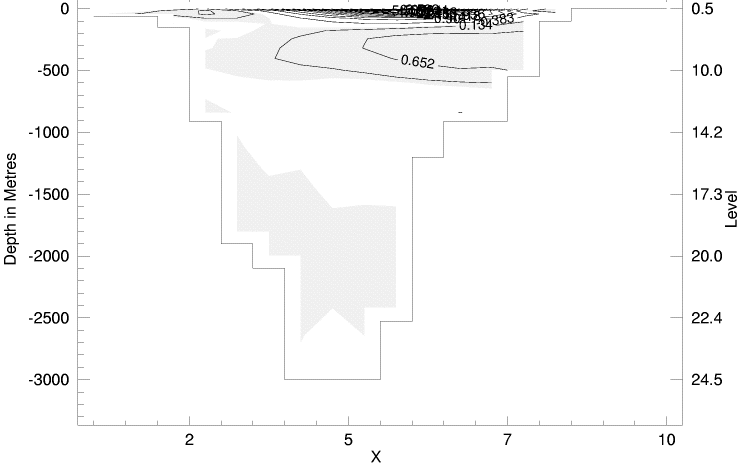 |
| data and inference |  |
 |
 |
The two IOS cases can be compared with each other, with results of other models, and with data and observational inference. April data for temperature and salinity are plotted from the Polar Science Center Hydrographic Climatology. Inferred circulation at intermediate depths (200 to 1700m) is from Rudels et al., 1994. A two-year average velocity from current meters across Fram Strait (along 79N) is from Dr. Eberhard Fahrbach.
What did we learn? The influence of single term, neptune, plays a large role in IOS circulation. Over the range of many models' results, the sense of circulation (more cyclonic or anticyclonic at 500m) varies greatly. Without neptune it is seen that IOS has broad, weak cyclonic circulation around the central Arctic, whereas neptune anchors the circulation in a way more like that suggested by Rudels et al. A second comparison is seen in the velocity section across Fram Strait where IOS changes from strongly horizontally sheared (with neptune) to weakly vertically sheared (without). Such remarks do not tend to validate (or invalidate) neptune but rather identify an aspect in which one model, IOS, differs from others. Many many differences affect model results. We see, e.g., that IOS suffers biases in temperature and salinity compared with observations.
A further study using AOMIP models examines the storage of heat and freshwater throughout the top 1000m of the Arctic. A pdf file (7 MB) can be downloaded.
to Planetwater |
 |
or | more research |
 |